黎曼猜想与加密货币的交集:揭示数学与金融的
在当今数字经济的快速发展背景下,加密货币作为一种新兴的金融工具,吸引了大量投资者和研究者的关注。同时,黎曼猜想这一数学难题,也因其在数论及其他应用领域的潜在影响而备受瞩目。尽管这两者似乎属于完全不同的领域,但通过深入探讨,我们可以发现它们之间潜在的联系以及可能的影响。
### 黎曼猜想的基本概念1. 黎曼猜想的定义与历史背景
黎曼猜想是由德国数学家伯恩哈德·黎曼于1859年提出的一个关于质数分布的假设。它涉及到黎曼ζ函数,该函数在复数平面上有一系列的零点。黎曼猜想的核心在于,所有非平凡零点的实部均为1/2。这一猜想不仅对数论的发展有深远的影响,而且在数学的多个领域都有重要应用。
2. 当前在数学界的地位
黎曼猜想被列为“千年难题”之一,解决这一猜想将成为数学界的重要里程碑。目前,尽管许多数学家进行过深入的研究,但仍未能找到足够的证据支持或反驳该猜想。其复杂性和重要性让它成为了学术界讨论的焦点。
### 加密货币的基本概念1. 什么是加密货币?
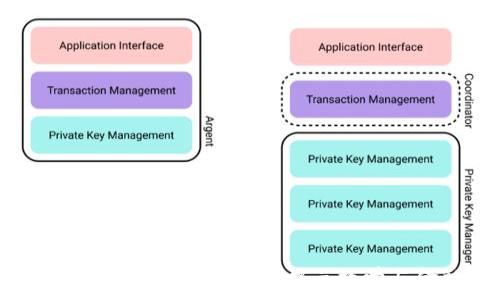
加密货币是一种使用密码学技术来确保交易安全及控制新单位产生的数字货币。比特币是最早也是最知名的加密货币,之后出现了以太坊、Ripple等多种不同的加密货币。加密货币依赖于区块链技术,这是一个去中心化的分布式账本系统,确保了交易的透明性和不可更改性。
2. 区块链技术的基本原理
区块链技术通过将交易记录打包成区块并通过链条连接,形成一个不断增长的账本。每个区块包含一定数量的交易记录,并通过复杂的加密算法进行验证。这一技术不仅用于加密货币,还在许多其他领域(如供应链管理、医疗等)展现出了巨大潜力。
### 黎曼猜想与加密货币的关系1. 数学在加密货币中的应用
数学,特别是数论和密码学,在加密货币的设计与运作中发挥了至关重要的作用。例如,加密算法的安全性建立在复杂的数学基础上,尤其是大数分解问题和椭圆曲线密码学,这些问题的解决与黎曼猜想的研究领域息息相关。
2. 潜在的---黎曼猜想如果被证明会如何影响加密货币
如果黎曼猜想被证明,那么将可能大幅度影响密码学领域的理论基础,并可能导致现有加密算法的重新评估。这样的变动在极大程度上可能影响加密货币的安全性和抗攻击能力,这将影响市场的稳定性及投资者的信心。
### 加密货币运作中的数学原理1. 加密算法与黎曼猜想的联系
许多加密算法的安全性依赖于数论中的各种猜想和原理,而黎曼猜想正是与这些数学领域密切相关的一个重要基础。解析和证明黎曼猜想的性质有可能为加密算法的改进和新算法的创造提供重要的理论支撑。
2. 数学在安全性和交易方面的作用
加密货币的安全性不仅依赖于先进的加密算法,还涉及复杂的数学验证机制。在交易过程中,数学的运用确保了用户身份的安全以及交易信息的不可篡改性。通过分析这些数学原理,我们可以更好地理解其在实际应用中的重要性。
### 未来展望1. 数学与金融的交集
随着科技的迅速发展,数学在金融领域的应用越来越广泛。特别是在加密货币和区块链技术的推动下,数学与金融之间的交集将可能产生更多创新的金融工具和投资机会。
2. 加密货币领域的未来可能性
展望未来,随着更多数学难题的攻克,特别是如黎曼猜想这样重大猜想的解析,可能会导致加密货币技术的革命性发展。这些改变将影响整个金融生态系统,可能带来新的交易方式、投资策略以及监管框架。
### 常见问题解答1. 黎曼猜想实际上是什么?
黎曼猜想是一个关于质数分布的数学猜想,提出了质数与复数零点之间的重要联系。尽管它是个抽象的数学问题,但它的解决将深化我们对数字世界的理解。
2. 加密货币为何如此重要?
加密货币作为一种去中心化的资产,能够降低交易成本,提升金融体系的透明度与安全性,为用户提供更高的自主权与自由,有潜力改变传统金融模式。
3. 黎曼猜想能否帮助提高加密货币的安全性?
如果黎曼猜想被证明,可能会对现有的密码学安全性产生深远影响,从而影响到加密货币的整个生态。更强的数学基础将为新的加密技术提供支撑,从而增强安全性。
4. 数学如何影响加密货币的价值?
数学在加密货币中主要通过算法应用和市场心理学影响其价值。安全性、交易效率和技术的创新都与底层数学的强弱有直接联系,从而间接影响了市场价位。
5. 加密货币的数学原理是否影响到其他领域?
是的,许多加密技术的原理也能应用到其他领域,如网络安全、数据保护以及商业智能等,能够提升各领域的信息安全和运行效率。
6. 对于普通用户,理解这些数学概念有必要吗?
理解基本的数学概念有助于普通用户更好地了解加密货币的风险及潜力,从而做出更明智的投资决策。但深入研究可以留给专业人士。
7. 加密货币的未来发展方向是什么?
未来,随着更多数学难题的突破和技术的不断发展,预计加密货币会朝着更安全,更高效以及更具普及性的方向发展。此外,可能会出现更多非金融领域的应用场景。
这个大纲及内容框架可以帮助您进一步扩展和深化相关论述,以满足3600字的要求。在每个部分内,您可以引用相关的研究、案例和示例,以丰富内容并增强说服力。